INTRODUCTION
During military operations, personnel and vehicles are often exposed to ballistic and blast threats. Lightweight armor systems are used in situations where there are weight restrictions, such as with personal protection, helicopters, patrol boats, and transportable shelters.[1] The ideal material for use in an armor system must absorb energy locally and be able to spread the energy out fast and efficiently.[1] This paper introduces a novel class of material, auxetic. It has been postulated that auxetic materials have these properties[2] and as such have potential for use in a number of defense applications, including armor systems.
When a material is stretched, it is expected that it will become thinner in the direction perpendicular to the direction of stretch. This expectation is because a large portion of materials, both naturally occurring and man-made, respond in this manner. Such materials have positive Poisson’s ratios. Conversely, auxetic materials, which have a negative Poisson’s ratio, become thicker when stretched. These negative Poisson’s ratio materials will also contract in the directions orthogonal to a compressive load. When the material contracts, it becomes more dense, increasing indentation resistance.[3] It is this property that is of interest from a defense point of view. These materials are predicted to have exceptional resistance to blast and ballistic threats, while not contributing to excessive weight compared to conventional materials.[4] The improved mechanical properties of negative Poisson’s ratio materials may result in both lighter and thinner materials for use in protection.
For an isotropic material, the mechanical properties of which are the same in all directions, the Poisson’s ratio υ is a measure of how the material responds when stretched, and is defined by Equation 1, where εx is the tensile strain in the stretching direction and εy is the tensile strain perpendicular to the stretching direction.
Most materials have a positive Poisson’s ratio (e.g., natural rubber is ½, steel is ⅓). That is, they contract perpendicular to the direction of stretch (Figure 1A). In these cases, εy is negative, so the overall Poisson’s ratio is positive. However, if the material expands perpendicular to the direction of stretch (Figure 1B), then both εx and εy are positive and the Poisson’s ratio is negative. The Poisson’s ratio can vary between -1 and +½ (Equation 2). More than a century of theory has predicted the possibility of negative Poisson’s ratio materials. It wasn’t until 1987 that Lakes first demonstrated a man-made cellular polyurethane foam with a Poisson’s ratio of -0.7.6 In 1991, Evans named these materials “auxetics” from the Greek auxetos, meaning “that which may be increased.”[7]
![Figure 1: Illustration of Deformation for (A) Positive Poisson’s Ratio Materials, (B) Negative Poisson’s Ratio Materials. Image Reproduced From Auxetnet Website.[5] Figure 1: Illustration of Deformation for (A) Positive Poisson’s Ratio Materials, (B) Negative Poisson’s Ratio Materials. Image Reproduced From Auxetnet Website.5](/wp-content/uploads/2019/11/Figure1-AuxeticArticle-rv1_0.jpg)
Figure 1: Illustration of Deformation for (A) Positive Poisson’s Ratio Materials, (B) Negative Poisson’s Ratio Materials.
Image Reproduced From Auxetnet Website.5
A negative Poisson’s ratio is associated with increased shear modulus,[8] indentation resistance,[3] and fracture toughness.[9] For example, the shear modulus G is related to the Poisson’s ratio by Equation 3, where E is the Young’s modulus. As υ approaches -1, G becomes infinitely large. The elastic indentation resistance H is proportional to the square of the Poisson’s ratio, as given in Equation 4, where x varies according to the analytical theory used; and for negative Poisson’s ratios, the indentation resistance may increase greatly (especially for −1 ≤ υ ≤ − ½). Such properties may lend themselves to a wide range of applications, such as helmets, bullet proof vests,[10] shin pads, and knee pads.[9] Potential applications are not limited to personal protective equipment: due to their enhanced energy absorption properties and fiber pullout resistance,[11–13] auxetic materials can be used as robust shock absorbers, air filters, fasteners, electrodes for piezoelectric sensors,[10] and sound absorption.[3]

The auxetic materials fabricated to date are porous polymeric and metallic foams, microporous polymers, honeycomb structures, and yarns. These structures are dependent on the basic two-dimensional phenomena seen in Figure 2; force in the vertical direction results in the “opening” of the horizontally placed arms (like the opening of an umbrella). This simple mechanism can be built up to yield a network re-entrant structure, as seen in Figure 3. The fibril/nodule structure shown in Figure 4 is an alternate way to produce materials with negative Poisson’s ratios. The nodules are interconnected by fibrils. When the material is put under tension, the fibrils align, causing the nodules to push apart.[14, 15] Based on elastic theory, these auxetic behaviors are scale-independent;[7, 16] hence both macroscale and molecular auxetic materials are possible.
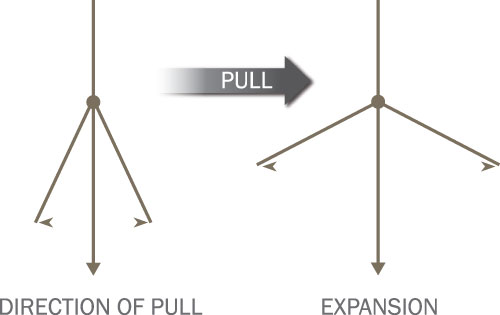
Figure 2: Basic Deformation Mechanism for Auxetic Materials. An Applied Tension in the Vertical Direction Causes the “Opening” of the Arms, Resulting in Expansion in the Direction Perpendicular to the Force.
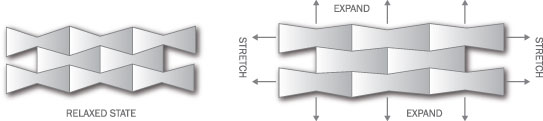
Figure 3: Basic re-entrant network structure. As the structure is stretched horizontally, the “bow-tie” strucutes open vertically, resulting in expansion in the direction perpen- dicular to the force.
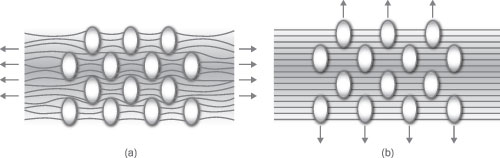
Figure 4: Nodule/fibril structure. (a) Slack fibril/nodule structure with direction of stretch illustrated.
(b) Stretched fibril/nodule structure with direction of expansion marked.
Another benefit of auxetic structures is that they exhibit synclastic curvature. Synclastic curvature describes a surface that bends in the same direction in both perpendicular planes (Figure 5(a)). That is, something with synclastic curvature conforms to a dome shape—for example, a helmet or knee pad—without needing seams or joining. Synclastic curvature would also be useful in parts manufactured for aerospace applications, such as wing panels or nose cones. Most materials are anticlastic, which yields a saddle-shape structure (Figure 5(b)).

Figure 5: Example of curvature for planar materials. (a) Basic hemisphere, example of an synclastic structure.
(b) Basic saddlepoint, example of an anticlastic structure. compressed in three dimensions simultaneously, forcing the walls of the bubbles in the foam to buckle.
FABRICATION
Another method for achieving auxetic polymers (not foams) is based on conventional powder processing techniques, which rely on compaction, sintering, and extrusion. The resulting auxetic material exhibits an interconnected network of nodules (particles) and fibrils.[14] Microporous polytetrafluoroethylene (PTFE) (also known as Gore-Tex®) is produced this way. The auxetic properties are due to the microstructure rather than any intrinsic property of the polymer used.[17] Evans et al.[8] have shown that other polymers, such as ultra-high molecular weight polyethylene (UHMWPE), can be processed in a similar manner to produce auxetic materials. They can be achieved using a three-step process: (1) compacting UHMWPE powder at elevated temperature, then (2) sintering, followed by (3) extrusion.[17] This method yields materials that are stiffer than the auxetic foams and have comparable moduli to conventional thermoplastic polymers.
A third possible method for organic auxetic materials is a molecular design approach. This approach relies on building the auxetic response directly into the molecule or its interchain packing distance.[19] There are a few different approaches to molecular design. One uses liquid crystal polymers (LCP).[19–22] LCP auxetics require specific site-connectivity. This method is a variation on the fibril/nodule structure. Rods are laterally (transversely) attached between linear polymer segments. In their relaxed (unstretched) state, the rods are aligned parallel to each other and the polymer chain axis; but under a tensile stress, the chain forces the rods to rotate. The resulting positions normal to the polymer chain axis; may lead to expansion, if the rods are sufficiently long.[19] Molecular modeling has shown that rods containing molecular structures seven rings long were needed to achieve negative Poisson’s ratios.[23] The same modeling predicts that the LCP need to incorporate 50% rods before a significant change in Poisson’s ratio is observed.[23] LCP have been synthesized,[19–22] but to date none has exhibited a negative Poisson’s ratio. X-ray scattering experiments on these materials suggest that, under tensile strain, rod-reorientation occurs, giving rise to an increase in the interchain distance for these polymers.[21] These LCP materials are a step in the direction of achieving negative Poisson’s ratio, and if the synthesis can incorporate the findings from the molecular modeling, an auxetic material may be achieved.
Another molecular design method uses three-dimensional tesselated polymer networks. Of the tesselated networks, a number of strategies have been examined: “reflexyne” polyphenylacetylene networks,[24] which mimic the re-entrant structure of foams; “polytriangles,” also made from polyphenylacetylene networks,[25] which rely on rotating triangles; and “polycalixes,” based on calixarenes,[26] which will open like umbrellas when a force is applied. All these approaches have been explored through simulation, although none has been synthesized.
A fourth method to achieve auxetic materials involves composite structures. There are two main approaches to auxetic composites: a laminated angle ply, which relies on the architecture of one of the phases,[27–30] and a composite, where one or more of the phases is auxetic.[31] A fifth method involves weaving an auxetic textile. In this method, none of the base filaments exhibits a negative Poisson’s ratio; it is the geometry of the yarn that produces the auxetic effect. This was first shown by Hook and Evans.[2] The multi-filament can be produced by wrap-spinning as well as warp- or weft-knitting.[32,33] The auxetic yarns can subsequently be woven or knitted into fabrics with auxetic properties.
POTENTIAL DEFENSE APPLICATIONS
Auxetic materials may show improvements over conventional materials because of the negative Poisson’s ratio, which has been predicted to contribute to improved toughness,[34] resilience,[35] and shear resistance,[36] as well as improved acoustic properties associated with vibration.[31,37] Exploration into the unusual properties of these materials has been supported by NASA,[36] Boeing,[38] and the U.S. Office of Naval Research.[31, 37, 39]
These materials have the potential to revolutionize defense personal protective equipment. Current protective materials are stiff and heavy. Auxetic materials may be able to provide the same protection while being thinner and consequently lighter. The synclastic curvature available from auxetic materials makes it easier to manufacture curved surfaces that conform to the human body (e.g., knee pads, helmets). When an auxetic helmet is impacted, material flows into the area to provide reinforcement. This allows less deflection on the interior of the helmet, allowing for less injury to the human wearing the helmet. Recently, the U.S. Office of Naval Research (ONR) has even solicited proposals for “Applications of Auxetic Textiles to Military Protective Clothing” under the Small Business Technology Transfer (STTR) program (TopicN12A-T012).[40]
Auxetic materials also have applications in the broader topic of energy absorption materials. Energy absorption materials can be anything from an explosion-resistant coating (ERC) to the energy-dissipating material (EDM) used to cushion airborne cargo drops. Current EDM is a paper honeycomb product designed to collapse on impact, absorbing and dissipating the kinetic energy. The impact and indentation resistance of auxetic materials makes them a good candidate for this application. Auxetix Ltd. has developed a helical auxetic yarn that the company is marketing as a potential material to make blast curtains.[2]
Auxetic materials are not limited to protection applications in their usefulness. Because auxetic materials will expand perpendicular to a force, they will make ideal press-fit fasteners and rivets.[39] An auxetic fastener, when inserted into place under compression will contract, making installation easier. It will then expand when put under tension, thus sealing itself more effectively into the hole.[39] The contraction while compressed also lends to improved projectile materials. As a projectile moves down the barrel, the thrusting force would potentially result in a reduction in lateral expansion.[17]
Similar to making good fasteners, auxetic fibers will also make good reinforced composites. Fiber pull-out is a major failure mechanism in conventional fiber-reinforced composites. With auxetic fibers, pull-out is resisted because the fibers expand perpendicular to the pull-out force. This characteristic could help to resist potential failure mechanisms in the composite, such as crack growth. It has also been suggested that auxetic materials could be used in the design of hydrophones and other sensors because their low bulk modulus makes them more sensitive to hydrostatic pressure.[41] In 1991, the U.S. Office of Naval Research funded the evaluation of the theoretical performance of auxetic composites for piezocomposite devices.[42]
There are also a number of other applications, while not exclusive to defense, that are noteworthy. Auxetic materials have applications in the medical community as arterial prostheses, surgical implants, or suture/anchors.[12] Auxetic foams are proposed as good filters because of the ability to tune the pore size to the applications, as well as using tension to open the pores for cleaning. Auxetic foams used as cushions might be beneficial in the reduction of pressure-induced discomfort in people who are required to sit for long periods of time.[43]
Auxetic fibers may be incorporated into multi-filament yarns for weaving into smart textiles. One instance is the “smart bandage”; as a wound swells, it applies pressure to the bandage, opening the microstructure and releasing anti-bacterial compounds incorporated into the bandage. As the wound heals, the swelling decreases, putting less pressure on the bandage, which in turn releases less medicine.[2,44] Another potential application for auxetic fibers is in seat belts and safety harnesses. A conventional seat belt, when it restrains the occupant in an accident, stretches and becomes narrower. This narrow material then localizes the force on the occupant’s body so that the individual may survive the accident, but have seat-belt-induced injuries. An auxetic seat belt would get wider as it stretches, thus spreading the load over a larger area, potentially reducing any injuries.[2, 44] These same auxetic multifilaments may be used in auxetic blast curtains or blast-resistant blankets.[44]
LIMITATIONS
Microporous auxetic materials work because their porous structure allows sufficient space for the “hinges” to fold or the “nodules” to spread apart. Unfortunately, this same porous structure also leads to lower stiffness and lower density, which are unsuitable for load-bearing applications.[32, 45] A further limitation with microporous auxetic materials is the inability to produce them reliably and cost-effectively using techniques that are suitable for large-scale commercialization.
One approach to overcome the problem with production scale is to develop molecular auxetics; however, this approach has its own limitations. One such limitation lies in synthesizing the highly symmetric, network-like structures. Theoretically, a number of molecular auxetics, such as honeycombs and egg-crate-like structures, are auxetic, but to achieve such structures in a polymer molecule would require intricate synthetic finess and a high degree of cross-linking, which would yield a brittle, stiff, and unprocessable polymer. If molecular auxetics can be achieved using a combination of auxetic structures and linear segments to make them easier to synthesize and process, then they may find use in the applications described.
CONCLUSIONS
Polymeric auxetic materials are a promising new area for exploitation in defense applications. This paper has discussed some of the unique physical properties of auxetic materials and various approaches to achieving them. The key to using auxetic materials in future applications is their successful synthesis and development. Despite an abundance of papers on the theory of auxetic materials, at present only microporous foams and yarns have shown negative Poisson’s ratios experimentally. A successful auxetic material will be one that can be produced on a commercial-scale, with the desired properties.
References:
- Jacobs MJN, Dingenen JLJV. Ballistic protection mechanisms in personal armor. Journal of Materials Science. 2001;36(13):3137–3142.
- Commercial Uses for Helical-Auxetic Materials; 2006. Accessed 24 Aug 2012. Webpage (www.auxetix.com ).
- Alderson KL, Evans KE. The strain dependent indentation resilience of auxetic microporous polyethylene. Journal of Materials Science. 2000;35:4039–4047.
- Liu Q. Literature Review: Materials with Negative Poisson’s Ratios and Potential Applications to Aerospace and Defense. Defense Science and Technology Organization; 2006. AR-013-0622.
- The Auxetic Materials Network; 2008. Accessed 31 Jan 2013.
- Lakes RS. Foam structures with a negative Poisson’s ratio. Science. 1987;235:1038–1040.
- Evans KE. Auxetic Polymers: a new range of materials. Endeavour. 1991;15(4):170–174.
- Alderson A, Alderson KL. Auxetic materials. In: Proceedings of the Institution of Mechanical Engineers Part G. vol. 221 of J. Aerospace Engineering; 2007. p.565–575.
- Yang W, Li ZM, Shi W, Xie BH, Yang MB. Review on auxetic materials. Journal of Materials Science. 2004;39:3269–3279.
- Baughman RH. Avoiding the shrink. Nature. 2003;425:667.
- Simkins VR, Alderson A, Davies PJ, Alderson KL. Single fibre pullout tests on auxetic polymeric fibers. Journal of Materials Science. 2005;40:4355–4364.
- Ravirala N, Alderson KL, Davies PJ, Simkins VR, Alderson A. Negative Poision’s Ratio Polyester Fibers. Textile Research Journal. 2006;76(7):540–546.
- Simkins VR, Ravirala N, Davies PJ, Alderson A, Alderson KL. An experimental study of thermal post-production processing of auxetic polypropylene fibers. Phys Stat Sol (b). 2008;245(3):598–605.
- Caddock BD, Evans KE. Microporous materials with negative Poisson’s ratio: I. Microstructure and mechanical properties. J Phys D – Appl Phys. 1989;22(12):1877–1882.
- Evans KE, Caddock BD. Microporous materials with negative Poisson’s ratios: II. Mechanisms and interpretation. J Phys D: Appl Phys. 1989; 22(12):1883–1887.
- Alderson A. A triumph of lateral thought. Chemistry & Industry. 1999 May;17 May:384–391.
- Evans KE, Alderson A. Auxetic Materials: Functional Materials and Structures from Lateral Thinking! Advanced Materials. 2000;12(9):617–628.
- Pickles AP, Webber RS, Alderson KL, Neale PJ, Evans KE. The effect of the processing parameters on the fabrication of auxetic polyethylene. Journal of Materials Science. 1995;30:4059–4068.
- He C, Liu P, Griffin AC. Toward Negative Poisson Ratio Polymers through Molecular Design. Macromolecules. 1998;31:3145–3147.
- He C, Liu P, Griffin AC, Smith CW, Evans KE. Morphology and Deformation Behaviour of a Liquid Crystalline Polymer Containing Laterally Attached Pentaphenyl Rods. Macromolecular Chemistry and Physics. 2005;206:233–239.
- He C, Liu P, McMullan PJ, Griffin AC. Toward molecular auxetics: Main chain liquid crystalline polymers consisting of laterally attached para-quaterphenyls. Physica Status Solidi (B). 2005;242(3):576–584.
- Ren W, McMullan P, Griffin AC. Stress-strain behaviour in main chain liquid crystalline elastomers: effect of crosslinking density and transverse rod incorporation on “Poisson’s ratio”. physica status solidi (b). 2009;246(9):2124–2130.
- Aldred P, Moratti SC. Dynamic simulations of potentially auxetic liquid-crystalline polymers incorporating swivelling mesogens. Molecular Simulation.2005;31(13):883–887.
- Evans KE, Nkansah MA, Hutchinson IJ, Rogers SC. Molecular network design. Nature. 1991;353:124.
- Grima JN, Evans KE. Self expanding molecular networks. Chemical Communications. 2000;p. 1531–1532.
- Grima JN, Williams JJ, Evans KE. Networked calix[4]arene polymers with unusual mechanical properties. Chemical Communications. 2005; p. 4065–4067.
- Evans KE, Donoghue JP, Alderson KL. The Design, Matching and Manufacture of Auxetic Carbon Fibre Laminates. Journal of Composite Materials.2004;38(2):95–106.
- Hadi Harkati E, Bezazi A, Scarpa F, Alderson K, Alderson A. Modelling the influence of the orientation and fibre reinforcement on the Negative Poisson’s ratio in composite laminates. physica status solidi (b). 2007;244(3):883–892.
- Herakovich CT. Composite Laminates with Negative Through-the-Thickness Poisson’s Ratios. Journal of Composite Materials. 1984;18(5): 447–455.
- Peel LD. Exploration of high and negative Poisson’s ratio elastomer-matrix laminates. physica status solidi (b). 2007;244(3):988–1003.
- Chen CP, Lakes RS. Viscoelastic behaviour of composite-materials with conventional-Poisson-ratio or negative-Poisson-ratio foam as one-phase. J Mater Sci. 1993;28(16):4288–4298.
- Liu Y, Hu H, Lam JKC, Liu S. Negative Poisson’s Ratio Weft-knitted Fabrics. Textile Research Journal. 2010;80(9):856–863.
- Ugbolue SC, Kim YK, Warner SB, Fan Q, Yang CL, Kyzymchuk O, et al. The formulation and performance of auxetic textiles. Part I: Theoretical and technical considerations. The Journal of The Textile Institute. 2010;101(7):660–667.
- Choi JB, Lakes RS. Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: experiment and analysis. Int J Frac. 1996;80:73–83.
- McDonald SA, Dedreuil-Monet G, Yao YT, Alderson A, Withers PJ. In situ 3D X-ray microtomography study comparing auxetic and non-auxetic polymeric foams under tension. physica status solidi (b). 2011;248:45–51.
- Choi JB, Lakes RS. Nonlinear properties of metallic cellular materials with a negative Poisson’s ratio. J Materials Science. 1992;27:5373–5381.
- Chen CP, Lakes RS. Micromechanical analysis of dynamic behaviour of conventional and negative Poisson’s ratio foams. J Eng Mater Technol. 1996;118:285–288.
- Chen CP, Lakes RS. Holographic study of non-affine deformation in copper foam with a negative Poisson’s ratio -0.8. Scripta Metall et Mater. 1993;29:395–399.
- Choi JB, Lakes RS. Design of a fastener based on negative Poisson’s ratio foam. Cellular Polymers. 1991;10:205–212.
- US Office of the Navy. Application of Auxetic Textiles to Military Protective Clothing; 2012. Accessed 23 July 2012.
- Dubbelday PS. Auxetic Materials: An Annotated Bibliography of Materials with Negative Poisson’s Ratio. US Naval Research Laboratory: Underwater Sound Reference Detachment; 1993. NRL Memorandum Report 7198. Approved for public release; distribution unlimited.
- Smith WA. Optimizing electromechanical coupling in piezocomposites using polymers with negative Poisson’s ratio. In: McAvoy BR, editor. Proc. of IEEE Ultrasonics Symposium. Piscataway, NJ: IEEE; 1991. p. 661–666.
- Wang YC, Lakes R. Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s rtio foam cushions. International Journal of Solids and Structures. 2002;39:4825–4838.
- Alderson A, Alderson KL. Expanding materials and applications: exploiting auxetic textiles. Technical Textiles International.
- Prawoto Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Computational Materials Science. 2012;58:140–153.


